Pessic de Matemàtiques 0015

PM0015

Situació relativa dels punts de pla respecte a una recta continguda en ell.

 r és una recta del pla d’equació a . x + b . y = c. Aquesta recta r divideix el pla en dos semiplans S₁ i S₂ . Si ( x₀ , y₀ ) és un punt del pla, passarà una de les tres coses següents:

a . x + b . y = c
a . x + b . y < c
a . x + b . y > c

Si a . x + b . y = c , el punt ( x₀ , y₀ ) està sobre la recta.
Si a . x + b . y < c , el punt ( x₀ , y₀ ) no està sobre la recta. Està en un dels dos semiplans. posem que està sobre S₁ . Llavors:
S₁ està format per tots els punts ( x , y ) del pla tals que a . x + b . y < c , i cap més.
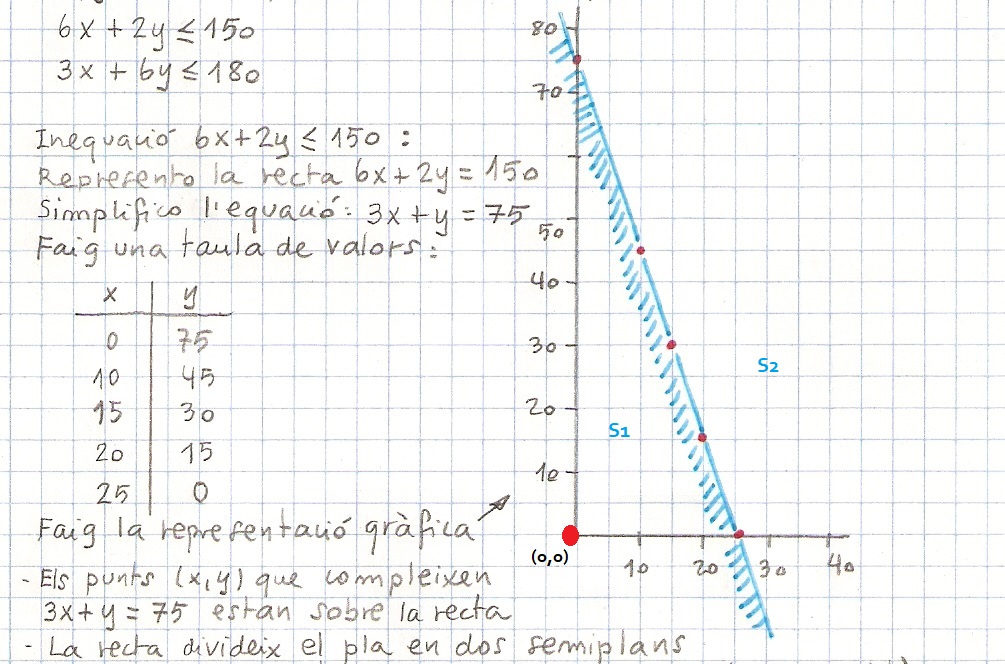
L’altre semiplà S₂ està format per tots els punts ( x , y ) del pla tals que a . x + b . y > c , i cap més.Exemple: Si r és la recta d’equació 6 . x + 2 . y = 150

Dic S₁ al semiplà que està per sota i a l’esquerra de r i S₂ a l’altre semiplà.
El punt ( 0 , 0 ) és a S₁
6 . 0 + 2 . 0 < 150
El semiplà S₁ està format per tots els punts ( x , y ) del pla que compleixen 6 . x + 2 . y < 150 i cap més.
El semiplà S₂ està format per tots els punts ( x, y ) del pla que compleixen 6 . x + 2 . y > 150 i cap més.

Altres Pessics de Matemàtiques relacionats amb aquest: